tkz-elements examples
Inner Circles
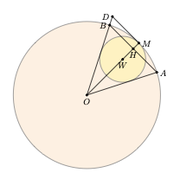
Example 1 Inner circle in an angular sector
View TeX code
% !TEX TS-program = lualatex
% Created by Alain Matthes on 2025.06.
\directlua
View Lua code
init_elements() z.O = point(0, 0) z.T = point(4, 0) C.OT = circle(z.O, z.T) z.A = C.OT:point(0.05) z.B = C.OT:point(0.20) z.M = C.OT:midarc(z.A, z.B) _,C.inner = line(z.O, z.A):c_ll_p(z.B, z.M) z.W = C.inner:get() z.H = intersection(line(z.A, z.B), line(z.O, z.M)) L.pp = line(z.A, z.B):parallel_from(z.M) z.D = intersection(L.pp, line(z.O, z.B))
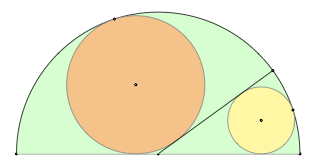
Example 2 Inners circles in a semi-circle.
View TeX code
% !TEX TS-program = lualatex
% Created by Alain Matthes on 2025.06.
\directlua
View Lua code
init_elements() local pos = ... z.A = point(0,0) z.B = point(10,0) L.AB = line(z.A, z.B) z.M = L.AB.mid C.MB = circle(z.M, z.B) z.X1 = point(8, 0) L.X1X2 = L.AB:orthogonal_from(z.X1) --z.P = intersection(L.X1X2, C.MB) z.P = C.MB:point(pos) T.AMP = triangle(z.A, z.M, z.P) L.MX3 = T.AMP:bisector(z.M) z.C = intersection(L.MX3, C.MB) T.PMB = triangle(z.P, z.M, z.B) L.MX4 = T.PMB:bisector(z.M) z.E = intersection(L.MX4, C.MB) C.one, C.two = line(z.M, z.A):c_ll_p(z.P, z.C) z.O1, _ = C.two:get() C.one, C.two = line(z.M, z.B):c_ll_p(z.P, z.E) z.O2, _ = C.two:get()