Skip to content

Pappus

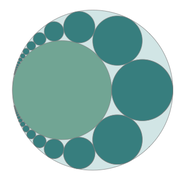
Example 1 Pappus chain with tkz-elements

In geometry, the Pappus chain is a ring of circles between two tangent circles investigated by Pappus of Alexandria in the 3rd century AD. Wikipedia

Example 1.

[PDF] [TEX] [LUA]

View TeX code 
% !TEX TS-program = lualatex
% Created by Alain Matthes on 2025-06-15.
% Copyright (c) 2025 __ AlterMundus __.
\documentclass[margin=12pt]{standalone} 
\usepackage[dvipsnames,svgnames]{xcolor}
\usepackage[mini]{tkz-euclide}
\usepackage{tkz-elements}
\begin{document}

\def\nc{16}
\def\xC{10}
\directlua{loadfile("pappus1.lua")(\xC, \nc)}

\begin{tikzpicture}
   \tkzGetNodes
   \tkzDrawCircle[fill=teal!20](i,C)
   \tkzDrawCircle[fill=PineGreen!60](j,B)
   \foreach \i in {-\nc,...,0,...,\nc} {
   \tkzDrawCircle[fill=teal]({I\i},{S\i'})
   }
\end{tikzpicture}
\end{document}
View Lua code 
init_elements()
local xC, nc = ...
local xB = xC / tkz.phi
local xD = (xC * xC) / xB
local xJ = (xC + xD) / 2
local r = xD - xJ
z.A = point(0, 0)
z.B = point(xB, 0)
z.C = point(xC, 0)
L.AC = line(z.A, z.C)
z.i = L.AC.mid
L.AB = line(z.A, z.B)
z.j = L.AB.mid
z.D = point(xD, 0)
C.AC = circle(z.A, z.C)
for i = -nc, nc do
  z["J" .. i] = point(xJ, 2 * r * i)
  z["H" .. i] = point(xJ, 2 * r * i - r)
  z["J" .. i .. "p"], z["H" .. i .. "p"] = C.AC:inversion(z["J" .. i], z["H" .. i])
  L.AJ = line(z.A, z["J" .. i])
  C.JH = circle(z["J" .. i], z["H" .. i])
  z["S" .. i], z["T" .. i] = intersection(L.AJ, C.JH)
  z["S" .. i .. "p"], z["T" .. i .. "p"] = C.AC:inversion(z["S" .. i], z["T" .. i])
  L.SpTp = line(z["S" .. i .. "p"], z["T" .. i .. "p"])
  z["I" .. i] = L.SpTp.mid
end



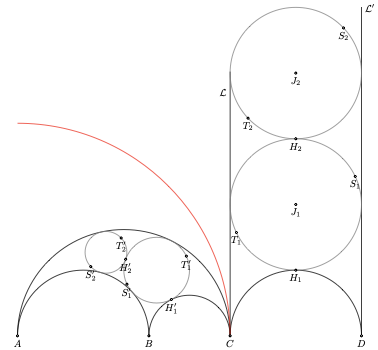
Example 2 Pappus explanations with tkz-elements

Let $D$ belong to the line $(AC)$ such that DB \cdot DA = AC^2$ then $B$ is the image of $D$ in the inversion of center $A$ and power $AC^2$. The semicircles of diameter $[AB]$ and $[AC]$ pass through the pole $A$. Their images are $\mathcal{L'}$ and $\mathcal{L}$. Circles of center $J_i$ and diameter $S_iT_i$ have as images circles of diameter $S'_iT'_i$.

Example 2.

[PDF] [TEX] [LUA]

View TeX code 
% !TEX TS-program = lualatex
% Created by Alain Matthes on 2022-01-18.
% Copyright (c) 2022 __ AlterMundus __.
\documentclass{standalone} 
\usepackage[dvipsnames,svgnames]{xcolor}
\usepackage[mini]{tkz-euclide}
\usepackage{tkz-elements}

\begin{document}
\def\nc{2} 
\def\xC{10}  
\directlua{loadfile("pappus-exp.lua")(\xC, \nc)}

\begin{tikzpicture}[scale=.75]
  \tkzGetNodes
  \tkzDrawLines[add=0 and 2.25](C,c)
  \tkzDrawLines[add=0 and 1.5](D,d)
  \tkzDrawSemiCircle(mAC,C)
  \tkzDrawSemiCircle(mAB,B)
  \tkzDrawSemiCircle(mBC,C)
  \tkzDrawSemiCircle(mCD,D)
  \tkzDrawArc[red](A,C)(a)
  \tkzDrawPoints(A,B,C,D)
  \tkzLabelPoints(A,B,C,D)
  \tkzLabelLine[left,pos=3](C,c){$\mathcal{L}$}
  \tkzLabelLine[right,pos=2.5](D,d){$\mathcal{L'}$}
  \foreach \i in {1,...,\nc}{
    \tkzDrawCircle(J\i,H\i)
    \tkzDrawCircle(I\i,T\i')
    \tkzDrawPoints({J\i},{H\i},{H\i'},{S\i},{S\i'},{T\i},{T\i'})
    \tkzLabelPoint(J\i){$J_\i$}
    \tkzLabelPoint(S\i){$S_\i$}
    \tkzLabelPoint(T\i){$T_\i$}
    \tkzLabelPoint(H\i){$H_\i$}
    \tkzLabelPoint(S\i'){$S'_\i$}
    \tkzLabelPoint(T\i'){$T'_\i$}
    \tkzLabelPoint(H\i'){$H'_\i$}
   }
\end{tikzpicture}
\end{document}
View Lua code 
init_elements()
local xC, nc = ...
local xB = xC / tkz.phi
local xD = (xC * xC) / xB
local xJ = (xC + xD) / 2
local r = xD - xJ
z.A = point(0, 0)
z.B = point(xB, 0)
z.C = point(xC, 0)
L.AC = line(z.A, z.C)
-- z.B = L.AC:gold_ratio()
z.D = point(xD, 0)
z.c = z.C:rotation(-math.pi / 2, z.B)
z.a = z.A:rotation(math.pi / 2, z.C)
z.d = z.D:rotation(-math.pi / 2, z.C)
L.AC = line(z.A, z.C)
z.mAC = L.AC.mid
L.AB = line(z.A, z.B)
z.mAB = L.AB.mid
L.BC = line(z.B, z.C)
z.mBC = L.BC.mid
L.CD = line(z.C, z.D)
z.mCD = L.CD.mid
C.AC = circle(z.A, z.C)
for i = 1, nc do
  z["J" .. i] = point(xJ, 2 * r * i)
  z["H" .. i] = point(xJ, 2 * r * i - r)
  z["J" .. i .. "p"], z["H" .. i .. "p"] = C.AC:inversion(z["J" .. i], z["H" .. i])
  L.AJ = line(z.A, z["J" .. i])
  C.JH = circle(z["J" .. i], z["H" .. i])
  z["S" .. i], z["T" .. i] = intersection(L.AJ, C.JH)
  z["S" .. i .. "p"], z["T" .. i .. "p"] = C.AC:inversion(z["S" .. i], z["T" .. i])
  L.SpTp = line(z["S" .. i .. "p"], z["T" .. i .. "p"])
  z["I" .. i] = L.SpTp.mid
end