Skip to content

tkz-euclide examples

Archimedes

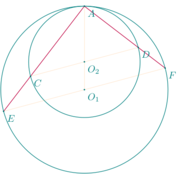
Example 1 Proposition 1 of the Book of Lemmas

If two circles touch at $A$, and if $[CD]$, $[EF]$ be parallel diameters in them, $A$, $C$ and $E$ are aligned.

Example 1.

[PDF] [TEX]

View TeX code 
\documentclass{standalone} 
\usepackage{tkz-euclide}
\tkzSetUpPoint[size=1,color=teal]
\tkzSetUpLine[thin,color=teal]
\tkzSetUpCompass[color=orange,ultra thin,/tkzcompass/delta=10]
\tikzset{label style/.append style={color=teal}}
\tikzset{new/.style={color=orange,ultra thin}} 

\begin{document} 
\begin{tikzpicture}
  \tkzDefPoints{0/0/O_1,0/1/O_2,0/3/A}
  \tkzDefPoint(15:3){F}
  \tkzInterLC(F,O_1)(O_1,A) \tkzGetSecondPoint{E}
  \tkzDefLine[parallel=through O_2](E,F) 
  \tkzGetPoint{x}   
  \tkzInterLC(x,O_2)(O_2,A) \tkzGetPoints{D}{C} 
  \tkzDrawCircles(O_1,A O_2,A)
  \tkzDrawSegments[new](O_1,A E,F C,D)
  \tkzDrawSegments[purple](A,E A,F)
  \tkzDrawPoints(A,O_1,O_2,E,F,C,D)
  \tkzLabelPoints(A,O_1,O_2,E,F,C,D)
\end{tikzpicture}
\end{document}

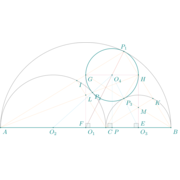
Example 2 Proposition 6 of the Book of Lemmas

Let $[AB]$, the diameter of a semicircle, be divided at $C$ so that $AC = \varphi·CB$ [or in any ratio]. Describe semicircles within the first semicircle and on $[AC]$, $[CB]$ as diameters, and suppose a circle drawn touching the all three semicircles. If $[GH]$ be the diameter of this circle, to find relation between $GH$ and $AB$.

Example 2.

[PDF] [TEX]

View TeX code 
\documentclass{standalone} 
\usepackage{tkz-euclide}
\tkzSetUpPoint[size=1,color=teal]
\tkzSetUpLine[thin,color=teal]
\tkzSetUpCompass[color=orange,ultra thin,/tkzcompass/delta=10]
\tikzset{label style/.append style={color=teal}}
\tikzset{new/.style={color=orange,ultra thin}} 
\tikzset{step 1/.style={color=cyan,ultra thin}} 
\tikzset{step 2/.style={color=purple,ultra thin}}

\begin{document} 
\begin{tikzpicture}[scale=1, /pgf/fpu/install only={reciprocal}]
   \tkzDefPoints{0/0/A,10/0/B}  
   \tkzDefGoldenRatio(A,B)                            \tkzGetPoint{C}
   \tkzDefMidPoint(A,B)                               \tkzGetPoint{O_1}
   \tkzDefMidPoint(A,C)                               \tkzGetPoint{O_2}
   \tkzDefMidPoint(C,B)                               \tkzGetPoint{O_3}
   \tkzDefExtSimilitudeCenter(O_2,A)(O_3,C)           \tkzGetPoint{M_0}
   \tkzDefIntSimilitudeCenter(O_1,A)(O_2,A)           \tkzGetPoint{M_1}
   \tkzDefIntSimilitudeCenter(O_1,B)(O_3,B)           \tkzGetPoint{M_2}
   \tkzInterCC(O_2,A)(M_2,B)                          \tkzGetFirstPoint{P_2}
   \tkzInterCC(O_3,B)(M_1,A)                          \tkzGetSecondPoint{P_3}
   \tkzInterCC(O_1,A)(M_0,C)                          \tkzGetFirstPoint{P_1}
   \tkzInterLL(O_2,P_2)(O_3,P_3)                      \tkzGetPoint{O_4}
   \tkzInterLC[common = P_1](A,P_1)(O_4,P_1)          \tkzGetFirstPoint{G}
   \tkzInterLC[common = P_1](B,P_1)(O_4,P_1)          \tkzGetFirstPoint{H}
   \tkzDefPointsBy[projection = onto A--B](O_4,G,H){P,F,E}
   \tkzInterLL(B,G)(H,E)                              \tkzGetPoint{M}
   \tkzInterLL(A,H)(G,F)                              \tkzGetPoint{L}
   \tkzInterLC[common = C](M,C)(O_3,C)                \tkzGetFirstPoint{K}
   \tkzInterLC[common = C](L,C)(O_2,C)                \tkzGetFirstPoint{I}
   \tkzDrawCircles(O_4,P_2)
   \tkzDrawSemiCircles[](O_1,B O_2,C O_3,B)
   \tkzDrawSegments(A,B)
   \tkzDrawSegments[step 1](O_4,P O_4,O_1 O_4,O_2 O_4,O_3)
   \tkzDrawSegments[new](A,P_1 P_1,B B,G A,H O_1,P_1)
   \tkzDrawSegments[new](C,H C,I C,K)
   \tkzDrawSegments[step 2](F,G G,H H,E O_1,P_1)
   \tkzDrawPoints(A,B,C,O_4,P_1,G,H,P,O_1,O_2,O_3,F,E,L,M,P_3,P_2,K,I)
   \tkzLabelPoints(A,B,C,G,H,P,O_4,O_1,O_3,L,M,P_3,P_2,K,I)
   \tkzLabelPoints[above](P_1)
   \tkzLabelPoints[below](O_2)
   \tkzLabelPoints[above right](E)
   \tkzLabelPoints[above left](F)
   \tkzMarkRightAngles[fill=teal!15,opacity=.4](B,F,G O_1,P,O_4 H,E,P)
\end{tikzpicture}

\end{document}