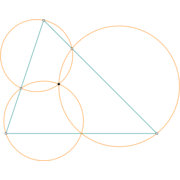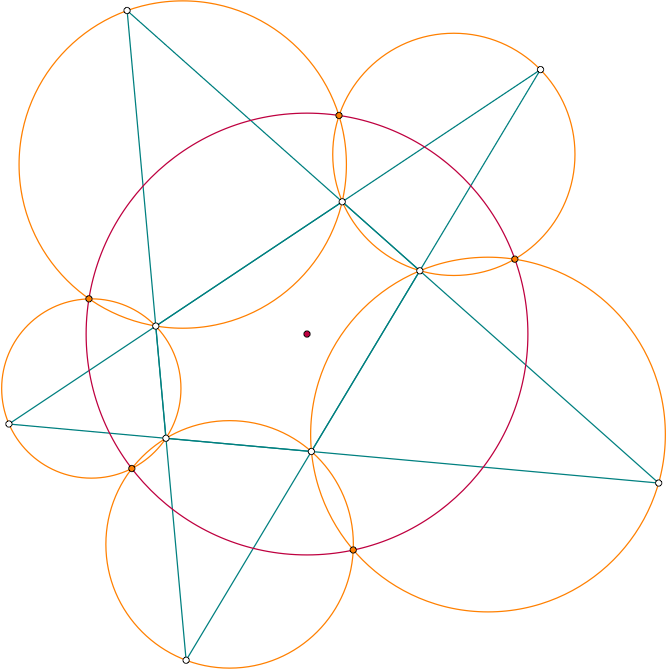Auguste Miquel
Example 1 Miquel point and Miquel circles
Miquel's theorem: For any triangle ABC and any three points a on (BC), b on (AC), and c on (AB), the three Miquel circles are the circles passing through each triangle vertex and the two points on its adjacent sides (i.e., Acb, Bac, and Cab). According to Miquel's theorem, the Miquel circles are concurrent in a point M known as the Miquel point.
Reciprocal: If three circles meet at a point M, we call a,b and c the other points of intersection of circles. Let A be a point on the first circle such that the line (MA) intersects (C2) at B and the line (PA) intersects (C3) at C. Miquel's theorem then states that the points B, a and C are aligned.
[PDF] [TEX]
View TeX code
\documentclass{standalone}
\usepackage{tkz-euclide}
\begin{document}
\begin{tikzpicture}
\tkzDefPoints{0/0/A,8/0/B,2/6/C}
\tkzDefPointWith[colinear=at C,K=.25](C,B)\tkzGetPoint{A'}
\tkzDefPointWith[colinear=at C,K=.6](C,A) \tkzGetPoint{B'}
\tkzDefPointWith[colinear=at A,K=.5](A,B) \tkzGetPoint{C'}
\tkzDefCircle[circum](A,C',B') \tkzGetPoint{x}
\tkzDefCircle[circum](B,A',C') \tkzGetPoint{y}
\tkzDefCircle[circum](C,A',B') \tkzGetPoint{z}
\tkzInterCC(x,A)(y,B) \tkzGetPoints{Q}{R}
\tkzDrawPolygon[teal](A,B,C)
\tkzDrawCircles[orange](x,A y,B z,C)
\tkzDrawPoints[fill=white](A,B,C,A',B')
\tkzDrawPoints[fill=black](Q)
\end{tikzpicture}
\end{document}
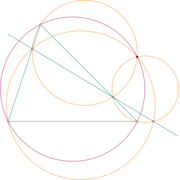
Example 2 Variation
Moreover, if a, b and c are chosen to be collinear then the point M lies on the circle defined by A, B and C.
[PDF] [TEX]
View TeX code
\documentclass{standalone}
\usepackage{tkz-euclide}
\begin{document}
\begin{tikzpicture}
\tkzDefPoints{0/0/A,8/0/B,2/6/C}
\tkzDefPointWith[colinear=at C,K=.75](C,B) \tkzGetPoint{a}
\tkzDefPointWith[colinear=at C,K=.25](C,A) \tkzGetPoint{b}
\tkzInterLL(a,b)(A,B) \tkzGetPoint{c}
\tkzDefCircle[circum](A,c,b) \tkzGetPoint{x}
\tkzDefCircle[circum](B,a,c) \tkzGetPoint{y}
\tkzDefCircle[circum](C,a,b) \tkzGetPoint{z}
\tkzDefCircle[circum](A,B,C) \tkzGetPoint{O}
\tkzInterCC(x,A)(y,B) \tkzGetPoints{M}{R}
\tkzDrawPolygon[teal](A,B,C)
\tkzDrawCircles[orange](x,A y,B z,C)
\tkzDrawPoints[fill=white](A,B,C,a,b,c)
\tkzDrawPoints[fill=black](M)
\tkzDrawCircle[purple](O,A)
\tkzDrawLine[teal](b,c)
\end{tikzpicture}
\end{document}
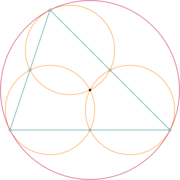
Example 3 Variation 2
Moreover, if a, b and c are chosen to be the midpoints of the sides of the triangle then the point M is also the center of the circumscribed circle of the triangle ABC.
[PDF] [TEX]
View TeX code
\documentclass{standalone}
\usepackage{tkz-euclide}
\begin{document}
\begin{tikzpicture}
\tkzDefPoints{0/0/A,8/0/B,2/6/C}
\tkzDefPointWith[colinear=at C,K=.5](C,B)\tkzGetPoint{a}
\tkzDefPointWith[colinear=at C,K=.5](C,A) \tkzGetPoint{b}
\tkzDefPointWith[colinear=at A,K=.5](A,B) \tkzGetPoint{c}
\tkzDefCircle[circum](A,c,b) \tkzGetPoint{x}
\tkzDefCircle[circum](B,a,c) \tkzGetPoint{y}
\tkzDefCircle[circum](C,a,b) \tkzGetPoint{z}
\tkzInterCC(x,A)(y,B) \tkzGetPoints{M}{R}
\tkzDrawPolygon[teal](A,B,C)
\tkzDrawCircles[orange](x,A y,B z,C)
\tkzDrawCircle[purple](M,A)
\tkzDrawPoints[fill=white](A,B,C,a,b,c)
\tkzDrawPoints[fill=black](M)
\end{tikzpicture}
\end{document}
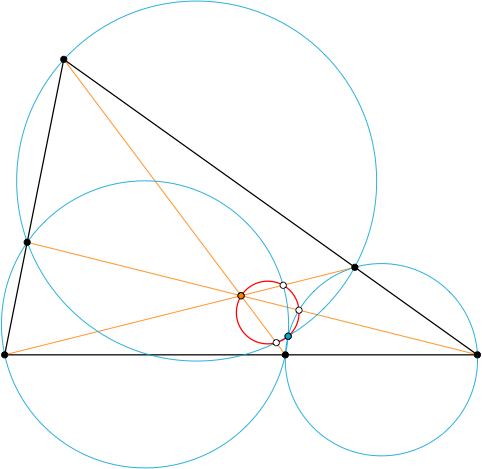
Example 4 Variation 3
Moreover, if a, b and c are the feet of Cevian lines through a point P then the points M and P lie on a circle UVW, where U is the intersection of (Aa) with circle Abc, V is the intersection of (Bb) with circle Bac and W is the intersection of (Cc) with circle Cab. [Christopher J Bradley Miquel circles and Cevian lines]
[PDF] [TEX]
View TeX code
\documentclass{standalone}
\usepackage{tkz-euclide}
\tikzset{step 1/.style={color=orange,thin}}
\tikzset{step 2/.style={color=cyan,thin}}
\begin{document}
\begin{tikzpicture}
\tkzDefPoints{0/0/A,8/0/B,1/5/C,4/1/P}
\tkzDrawPolygon(A,B,C)
\tkzInterLL(A,P)(B,C) \tkzGetPoint{a}
\tkzInterLL(B,P)(A,C) \tkzGetPoint{b}
\tkzInterLL(C,P)(B,A) \tkzGetPoint{c}
\tkzDefCircle[circum](A,c,b) \tkzGetPoint{x}
\tkzDefCircle[circum](B,a,c) \tkzGetPoint{y}
\tkzDefCircle[circum](C,a,b) \tkzGetPoint{z}
\tkzInterLC[common=A](A,P)(x,A) \tkzGetFirstPoint{U}
\tkzInterLC[common=B](B,P)(y,B) \tkzGetFirstPoint{V}
\tkzInterLC[common=C](C,P)(z,C) \tkzGetFirstPoint{W}
\tkzDefCircle[circum](U,V,W) \tkzGetPoint{O}
\tkzInterCC(x,A)(y,B) \tkzGetPoints{M}{R}
\tkzDrawSegments[step 1](A,a B,b C,c)
\tkzDrawCircles[step 2](x,A y,B z,C)
\tkzDrawCircle[red](O,U)
\tkzDrawPoints(A,B,C,a,b,c)
\tkzDrawPoints[fill=white](U,V,W,P,M)
\tkzDrawPoints[fill=orange](P)
\tkzDrawPoints[fill=cyan](M)
\end{tikzpicture}
\end{document}
Example 5 Complete quadrilateral theorem
A complete quadrilateral is a system of four lines, no three of which pass through the same point, and the six points of intersection of these lines.
The circumcircles of all four triangles of a complete quadrilateral meet at a point M.
[PDF] [TEX]
View TeX code
\documentclass{standalone}
\usepackage{tkz-euclide}
\begin{document}
\begin{tikzpicture}
\tkzDefPoints{0/0/A,5/2/B,3/8/F}
\tkzDefBarycentricPoint(A=1,F=3) \tkzGetPoint{D}
\tkzDefBarycentricPoint(F=1,B=2) \tkzGetPoint{C}
\tkzInterLL(D,C)(A,B) \tkzGetPoint{E}
\tkzDrawPolySeg[gray](A,E,D,F,B,A,D)
\tkzDefCircle[circum](F,D,C) \tkzGetPoint{x}
\tkzDefCircle[circum](A,D,E) \tkzGetPoint{y}
\tkzDefCircle[circum](A,B,F) \tkzGetPoint{z}
\tkzDefCircle[circum](B,E,C) \tkzGetPoint{t}
\tkzDefCircle[circum](x,y,z) \tkzGetPoint{M}
\tkzDrawCircles[orange](x,D y,A z,A t,B)
\tkzDrawCircles[cyan](M,x)
\tkzDrawPoints[fill=black](A,B,C,D,E,F)
\tkzDrawPoints[fill=orange](x,y,z,t)
\tkzDrawPoints[fill=cyan](M)
\tkzLabelPoints(A,B,C,D,E,F)
\end{tikzpicture}
\end{document}
Example 6 Miquel's pentagon theorem
Let be a convex pentagon. Extend all sides until they meet in five points and draw the circumcircles of the five triangles obtained. Then the second intersection points are concyclic.
[PDF] [TEX]
View TeX code
\documentclass{standalone}
\usepackage{tkz-euclide}
\begin{document}
\begin{tikzpicture}
\tkzDefPoints{0/-2/A,6/8/B,-3/2/C,8/1/D,-1/9/E}
\tkzInterLL(A,B)(D,E) \tkzGetPoint{F}
\tkzInterLL(E,D)(B,C) \tkzGetPoint{G}
\tkzInterLL(A,E)(B,C) \tkzGetPoint{H}
\tkzInterLL(A,E)(D,C) \tkzGetPoint{I}
\tkzInterLL(A,B)(D,C) \tkzGetPoint{J}
\tkzDefCircle(B,G,F) \tkzGetPoint{o1}
\tkzDefCircle(E,G,H) \tkzGetPoint{o2}
\tkzDefCircle(C,H,I) \tkzGetPoint{o3}
\tkzDefCircle(A,I,J) \tkzGetPoint{o4}
\tkzDefCircle(F,J,D) \tkzGetPoint{o5}
\tkzInterCC[common=G](o1,G)(o2,G) \tkzGetFirstPoint{K}
\tkzInterCC[common=H](o2,H)(o3,H) \tkzGetFirstPoint{L}
\tkzInterCC[common=I](o3,I)(o4,I) \tkzGetFirstPoint{M}
\tkzInterCC[common=J](o4,J)(o5,J) \tkzGetFirstPoint{N}
\tkzInterCC[common=J](o5,F)(o1,F) \tkzGetFirstPoint{O}
\tkzDefCircle(O,K,L) \tkzGetPoint{P}
\tkzDrawPolygons[teal](A,B,C,D,E F,G,H,I,J)
\tkzDrawCircles[orange](o1,B o2,E o3,C o4,A o5,D)
\tkzDrawCircle[purple](P,K)
\tkzDrawPoints[fill=white](A,...,J)
\tkzDrawPoints[fill=orange](K,...,O)
\tkzDrawPoints[fill=purple](P)
\end{tikzpicture}
\end{document}