Only Compass

Example 1

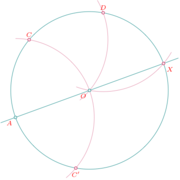
Construct on the circumference of a given circle a point diametrically opposite to a given point $A$. There are several methods, the one described is the best because the compass opening remains constant. Variation of the problem : Double, triple... multiply a given length by any integer.

[PDF] [TEX]

\documentclass{standalone} 
 \usepackage{tkz-euclide}
 \tkzSetUpPoint[size=3,color=teal,fill=teal!10]
 \tkzSetUpLine[line width=0.4pt,color=teal]
 \tkzSetUpCompass[color=red,ultra thick,delta=0]

 \begin{document} 
 \begin{tikzpicture}
 \def\r{3} \def\angle{200}
 \tkzSetUpArc[delta=10,color=purple,line width=.2pt]
 \tkzSetUpLabel[font=\scriptsize,red]
 \tkzDefPoint(0,0){O}
 \tkzDefPoint(\angle:\r){A}
 \tkzInterCC(O,A)(A,O) \tkzGetPoints{C'}{C}
 \tkzInterCC(O,A)(C,O) \tkzGetPoints{D'}{D}
 \tkzInterCC(O,A)(D,O) \tkzGetPoints{X'}{X}
 \tkzDrawCircle(O,A)
 \tkzDrawArc(A,C')(C)
 \tkzDrawArc(C,O)(D)
 \tkzDrawArc(D,O)(X)
 \tkzDrawLine[add=.1 and .1](A,X)
 \tkzDrawPoints(O,A)
 \tkzSetUpPoint[size=3,color=purple,fill=purple!10]
 \tkzDrawPoints(C,C',D,X)
 \tkzLabelPoints[below left](O,A)
 \tkzLabelPoints[below](C')
 \tkzLabelPoints[below right](X)
 \tkzLabelPoints[above](C,D)
 \end{tikzpicture}
 \end{document}