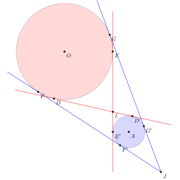
The point of intersection of the two crossing tangents is called the internal similitude center. The point of intersection of the extensions of the other two tangents is called the external similitude center.The code has been adapted for the latest version of tkz-euclide(5.10).
View TeX code
\documentclass{standalone}
\usepackage{tkz-euclide}
\begin{document}
\begin{tikzpicture}
\tkzDefPoints{0/0/O,4/-5/A}
\tkzDefCircle[R](O,3) \tkzGetPoint{To}
\tkzDefCircle[R](A,1) \tkzGetPoint{Ta}
\tkzDrawCircle[fill=red!50,opacity=.3](O,To)
\tkzDrawCircle[fill=blue!50,opacity=.3](A,Ta)
\tkzDefSimilitudeCenter[int](O,To)(A,Ta) \tkzGetPoint{I}
\tkzDefSimilitudeCenter[ext](O,To)(A,Ta) \tkzGetPoint{J}
\tkzDefTangent[from = I](O,To) \tkzGetPoints{D}{E}
\tkzDefTangent[from = I](A,Ta) \tkzGetPoints{D'}{E'}
\tkzDefTangent[from = J](O,To) \tkzGetPoints{F}{G}
\tkzDefTangent[from = J](A,Ta) \tkzGetPoints{F'}{G'}
\tkzDrawSegments[add = .5 and .5,color=red](D,D' E,E')
\tkzDrawSegments[add= 0 and 0.25,color=blue](J,F J,G)
\tkzDrawPoints(O,A,I,J,D,E,F,G,D',E',F',G')
\tkzLabelPoints(O,A,I,J,D,E,F,G,D',E',F',G')
\end{tikzpicture}
\end{document}